Data structures

An introduction to data structures...

A data structure is,

• A way of organizing and storing data

• define

  • the relationship between the data

  • the operations that can be performed on the data

• So that they can be accessed and worked with efficiently

---

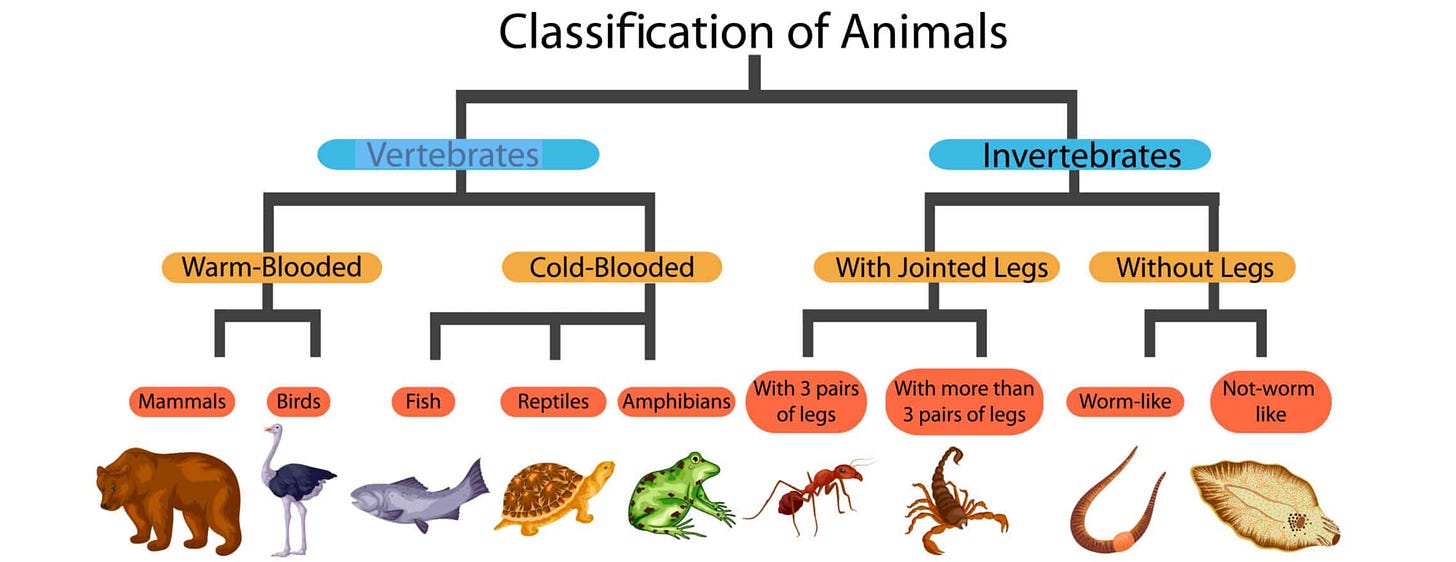
Data structures categorization

Data structures can be categorized in various ways based on different characteristics,

1. Primitive and Non-Primitive Data Structures

   • Primitive types: Basic data structures that are built-in or primitive within the system. Examples include numerical types (integers, floats), booleans, and characters.

   • Non-primitive types: These include more complex data structures, such as arrays, files, lists, trees, graphs, sets, tuples, dictionaries or hash tables, and more.

2. Linear and Non-Linear Data Structures

   • Linear: In linear data structures, elements are arranged sequentially and each element is connected to its previous and next element. Examples: Arrays, Linked Lists, Stacks, Queues.

   • Non-linear: In non-linear data structures, at least one element has multiple children. Examples: Trees, Graphs.

3. Static and Dynamic Data Structures

   • Static: The size and structure is fixed at compile time. Memory allocation is done at compile time. An example is an array.

   • Dynamic: The size and structure can be altered during runtime. Memory allocation is done at runtime. Examples include Linked List, Trees, Stack implemented using linked list, etc.

4. Homogeneous and Heterogeneous Data Structures

   • Homogeneous: All elements are of the same type. Examples: Array, Linked List.

   • Heterogeneous: A data structure that contains elements of different data types. Examples: Structures in C, Class in object-oriented programming languages.

5. Simple and Composite Data Structures

   • Simple: They contain values of the same type. Examples: Arrays, Lists.

   • Composite: They can hold values of different types. Examples: Structures, Objects in OOP.

6. In-Memory and Persistent Data Structures

   • In-Memory: These data structures exist in main memory. Examples: All data structures implemented in common programming languages typically.

   • Persistent: These survive beyond the lifetime of the process and are stored in non-volatile memories (like hard disk). Examples: B-Trees, Tries, used in databases and file systems.

The right data structure to use would depend on multiple factors including the specific use-cases or requirements of the algorithm or application.

---

Common types of data structures

1. Arrays

• An array stores a collection of items at adjoining memory locations. Items can be accessed using their indices.

• Because of their ability to use an index to directly access an element, arrays are often used when the size of the collection can be known in advance. They are frequently used in mathematical computations where accessing elements in a sequential manner is common. For instance, matrices, which are two-dimensional arrays, are often used in graphics transformations.

2. Linked Lists

• A linked list stores elements in a node. The node consists of two parts, i.e., data and the address to the next node in sequence.

• Linked lists are used when you want to add or remove elements from the list without worrying about the size of the list. They are often used to implement other data structures like stacks, queues, and even hash tables. In computer science, they can be used to represent sequences or lists of items.

3. Stacks

• A stack is a linear data structure that follows a particular order in which operations are performed. The order may be LIFO (Last In First Out) or FILO (First In Last Out).

• Stacks are used when you want to have access to elements in a Last-In-First-Out manner (LIFO). They're commonly used in scenarios like keeping track of memory during a recursive function call, undo operations in text editors, or in tree/graph traversal algorithms like depth-first-search.

4. Queues

• A Queue is a linear data structure that follows a particular order in which operations are performed. The order is First In First Out (FIFO).

• Queues are used when you want to have access to elements in a First-In-First-Out manner (FIFO). They're commonly used to handle asynchronous data transfers (like printing documents on a printer), or in scenarios that involve a processing order, such as serving requests on a single shared resource like a printer, CPU task scheduling, etc.

5. Trees

• A tree is a non-linear data structure that simulates a hierarchical tree structure with a set of linked nodes. It has one root node and zero or more subtrees.

Main types of trees:

1. Binary Tree: A binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child

2. Binary Search Tree (BST): Also known as ordered or sorted binary tree, is a type of binary tree where the nodes are arranged in order: for each node, all elements in the left subtree are less than the node, and all elements in the right subtree are greater than the node.

3. AVL Tree: A self-balancing binary search tree. The key feature of an AVL tree is that it tries to keep the 'balance' (i.e., the height difference of left subtree and right subtree) of every node not more than 1. This ensures all operations are performed in O(log n) time.

4. Red-Black Tree: A type of self-balancing binary search tree, where each node has an extra bit for denoting the color of the node, either red or black. The coloring and additional properties help keep the tree balanced during insertions and deletions, ensuring search, insertion, and deletion operations all take O(log n) time.

5. B-tree: They are generalization of a binary search tree that has a variable number of keys per node and keys are kept sorted. B-trees are sorted trees that are designed to work well on direct-access storage devices like magnetic disks. Databases and file systems often use B-trees, or variants.

6. Heap (Binary heap): A binary heap often represented as a complete binary tree with two key properties: shape property (maintains completeness) and heap property (parent node has a value less than or equal to (in a min-heap) or greater than or equal to (in a max-heap) its children). Main application is as an efficient priority queue.

6. Graphs

• A graph is an abstract data structure that represents connectivity between pairs of objects. A graph can be directed or undirected.

• Graphs are used to represent networks, including telephone networks and social networks. They're also used in mapping and routing algorithms, such as Google Maps' shortest path feature. Lastly, they're used in website crawlers by search engines to track all the connected links of a website.

7. Hashing

• In hashing, large keys are converted into small keys by using hash functions. The values are then stored in a data structure called a hash table.

• Hash tables, which use hash functions to efficiently store keys by their value, are used in databases for quick data retrieval. They're also often used in caches, to quickly store and retrieve data from memory.

8. Heaps

• Heaps are a type of binary tree. A heap is a special tree-based data structure in which the tree is a complete binary tree.

• Heaps are used in many algorithms such as HeapSort and in constructing priority queues. Heaps are also used in graph algorithms like Dijkstra's algorithm.

9. Tries

• A trie, also called a prefix tree, is a tree-like data structure that proves to be quite effective in solving problems related to strings.

• Tries are often used in searches where the key is a string, for auto-completion where you need to search for keys often, in IP routing to store routing information, etc

10. Matrices

• Matrices are a multi-dimensional array used to represent the relationship between multiple data items.

• A matrix is a grid of elements represented as rows and columns. It's technically a two-dimensional array, where each element is identified by two indices instead of just one.

• Matrices are often used in the fields of computer graphics, physics simulations, cryptography, machine learning and data science and more

The choice of a data structure depends on the problem that you are trying to solve, the ease of use, the efficiency in terms of space and time, among other factors.

---

Arrays

Arrays are one of the most commonly used data structures in programming. They are a way to store multiple items (elements) of the same datatype together in a contiguous block of memory. This collection allows a programmer to efficiently manage a group of variables of the same type by using a single name and an index (to indicate the position).

These are the various real-world use cases of arrays:

1. Storing and Processing Tabular Data: Arrays are used when you have a significant amount of data of the same type that can be stored in a table-like format. Examples include, but are not limited to, storing student grades, statistical data, or pixel values of an image.

2. Sorting and Searching: They are useful in arranging data in a specific order. This is primarily due to the fact that every element in the array is equally accessible, which makes sorting algorithms efficient.

3. Buffers: "Buffer" data structures that temporarily store data while it is being moved from one place to another are often implemented as arrays.

4. Multi-Dimensional Data: They are not limited to a single dimension. Instead, they can have multiple dimensions, making them suitable for mathematical computations on matrices.

5. Implementing Other Data Structures: Arrays can be used to implement other more complex data structures like Stack, Queue, Heap, Hash Map etc.

6. Lookup tables and Dictionaries: Arrays can be used to store records with keys and values where lookup operation is essential.

7. String Representation: In a lot of languages, strings are represented as an array of characters.

In brief, arrays are a fundamental data structure that provides an essential tool for managing multiple data items effectively and are a building block for more complex data structures. They have diverse applications across various fields like databases, algorithms, graphics, and many more.

Linked Lists

Linked Lists are a type of linear data structure, where each element (or node) contains a reference to the next node in the sequence. In a singly linked list, this connection is in one direction, and in a doubly linked list, nodes also reference the previous node. Here are some practical uses for linked lists:

1. Dynamic Memory Allocation: If we need a data structure whose size can change during runtime, linked lists are a good choice. Since they are not stored in contiguous memory locations, their size can be increased or decreased easily.

2. Implementing Stacks and Queues: Both stacks and queues can be easily implemented using linked lists. A stack is a LIFO (Last-In-First-Out) structure and a queue is a FIFO (First-In-First-Out) structure. For both of these use cases, elements can be added and removed efficiently from a linked list.

3. Graph Representations: Linked lists can be used to represent graphs. The nodes can represent graph vertices and the edges can be represented by links.

4. Polynomial Arithmetic: Linked lists are used in representing and manipulating polynomials. Each node can represent a term of the polynomial.

5. Creating Music Playlists: If you have ever used a music playlist, that's where linked lists come into action. Songs can be played in a sequence, shuffled or replayed again, you can also go to the next or the previous songs, all these operations can be implemented using a linked list, where each node points to the next song.

6. Navigation systems: Systems like web browser history for "back" and "forward" are implemented using doubly linked list, you can go back to the previous visited website, and also you can go forward.

Unlike arrays, linked lists have some overhead as they must store pointers to other nodes. However, because they're linked, it is easy to insert and delete nodes from them without having to shift or reorganize an entire block of memory. Also, unlike arrays, linked lists do not provide constant time access to a particular node. If you want to get to the nth node of a linked list, you have to start at the first node and follow the links until you get to the nth node.

Stacks

Stacks are a type of linear data structure that operate on the principle of LIFO (Last-In-First-Out), which means the last element added to the stack is the first one to be removed. In a physical analogy, you can think of it like a stack of plates. You add (push) a new plate to the top of the stack and also remove (pop) plates from the top of the stack.

Here are some of the many practical uses for stacks in software development:

1. Function Calls and Recursion: Stacks are used in function calls and recursion. When a function is called, the return address, data, etc., are pushed onto a call stack. When the called function has finished running, this data is then popped off the stack, and control goes back to the returned address.

2. Parsing: Stacks are used in compilers and parsers. For example, stacks are used for syntax checking of expressions like balanced symbols such as {}, [], () and so on.

3. Expression evaluation and Conversion: Stacks are used for evaluating prefix, infix and postfix arithmetic expressions. They are also used for converting an infix expression to postfix or prefix expressions.

4. Undo Operations: In many modern text editors or word processors, the "undo" operation can go back many steps, undoing a series of user actions. A stack can keep track of those actions as they occur, making it easy to "pop" the most recent action in order to undo it.

5. Depth-First Search (DFS): In tree or graph data structures, a depth-first search can be implemented using stacks.

6. Backtracking Algorithms: Backtracking algorithms like maze, finding paths, exhaustive search etc., often use stacks to store intermediate states.

Stacks are particularly useful when the exact number of elements in the collection is not known beforehand, and can change dynamically, but access to any elements other than the top one isn't required or can be restricted. The simple push and pop operations allow for efficient management of the collection with a LIFO access pattern.

Queues

Queues are a type of data structure that stores elements in a sequence in which operations are performed based on the First-In-First-Out (FIFO) principle. This means that the item that's been in a queue the longest, is the first one to get removed.

Here are some of the practical applications of queues in the real world:

1. Handling Asynchronous Tasks: In web development, a queue data structure can be used to handle asynchronous tasks, like sending emails, logging activity, etc. Tasks are added to the queue and are processed in the order they were added.

2. Scheduling in Operating Systems: Queues are widely used in operating system scheduling algorithms. Processes are scheduled based on their priorities (priority queues), or on a first-come basis (regular queues).

3. Breadth First Search (BFS): In graph theory, a breadth-first search algorithm uses a queue to visit nodes or vertices. It visits vertices in a breadthward motion and uses a queue to remember to get the next vertex to start the search when a dead-end occurs in any iteration.

4. Buffering in Data Communication and IO Buffers: Queues are used for buffering data in routers, streaming services, or print spooling. Data sent between two communication protocols is often of varying speeds. Thus, if the sending protocol produces data at a faster rate than the receiving protocol can consume, a buffer is used to queue up the sent data.

5. Waiting Calls: A good example of queue is the handling of waiting calls in a call center.

6. CPU Scheduling, Disk Scheduling: Where operations are backed up into a buffer and then scheduled based on priority, time of arrival, or other factors.

The essential feature of queue is that it inserts at the end and removes from the beginning, allowing it to maintain the FIFO structure. This orderly and disciplined process makes it applicable for scenarios where it's important to maintain the order of the elements.

Trees

Trees are a type of hierarchical data structure that represent relationships between objects in a hierarchical pattern. Each node in a tree has a parent node and zero or more children nodes (except for the root node, which has no parent). Trees are used in many fields of computer science, including operating systems, graphics, database systems, and computer networking.

Here are some real-world applications of trees:

1. Database Indexing: Trees, especially self-balancing Binary Search Trees like AVL trees and Red-Black trees, are commonly used in database and file-system indexing. These structures provide for fast searching, insertion, and deletion operations.

2. Compiler Design: Tree structures like Abstract Syntax Trees and Parse Trees are used in compiling process to parse source code into an intermediate form.

3. Networking: In computer networking, trees are used in the grouping or broadcasting operation. An example is the spanning tree protocol, which prevents looping in a network.

4. File Systems: Used in file directories where each folder is considered as a node and their sub-folders as their children.

5. Machine Learning: Decision Trees are used in machine learning algorithms to make predictions based on input features.

6. Game Programming: In game programming, trees can be used in decision making for AI, for example by using a game tree.

7. Hierarchical Data Representation: Trees are used when we want to represent data that naturally forms a hierarchy. For example, the HTML DOM is a tree structure.

8. Heap: Heap is a type of tree which is used to implement priority queues, which in turn are used in scheduling processes in operating systems.

Each of these examples utilizes the hierarchical and ordered nature of the tree data structure. The specific type of tree used (binary search tree, B-tree, trie, etc.) depends on the exact use case and the operations that need to be optimized.

Graphs

Graphs are a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. Graphs are used to solve many real-life problems as they can represent networks of various kinds.

Here are some real-world applications of graphs:

1. Social Networks: Graphs are the underlying data structure for social network platforms like Facebook, Twitter, Instagram, etc. People as nodes and their connections as edges.

2. Web Crawlers: Search engines use web crawlers that utilize graphs for web page traversal. A graph is formed by web pages as vertices and hyperlinks as edges.

3. Google Maps: Graphs are used in representing maps and finding paths. The Google Maps application uses the concept of graphs to find the shortest path or least time-consuming path.

4. Networking: Routers and connections between them form a graph, and different path finding algorithms are run on them to find the most efficient path or shortest path for data packet transmission.

5. Recommendation Engines: Recommendation engines use graph-based algorithms to recommend a new friend on Facebook or a new song on Spotify or a new product on Amazon.

6. Dependencies / prerequisites: Graphs can be used to represent systems with dependencies/prerequisites. An example is course prerequisites at a university.

7. Biology: In biology, graphs can be used to model structures like animal behavior or relationships, food webs, or population modelings.

8. Project Planning: In project planning, a dependency graph could be utilized to represent tasks and their dependencies.

Graphs are quite useful in representing and working with complex relationships between different components, modeling networks, and are used widely in solving problems across various domains, including computer science, physics, sociology, transportation, and others.

Hashing

Hashing is a technique that is used to uniquely identify a specific object from a group of similar objects. It's done using a function called a hash function which takes the data (key) and returns a hash, which is typically a number that corresponds to an index in an array (hash table).

Here are some real-life applications of hashing:

1. Database Indexing: Hashing is used in many database indexing algorithms to quickly locate an item in a database. A unique identifier of an item is passed through a hash function to generate a hash code.

2. Cryptography: In cryptography, hashing is used to generate a hash from the input which is almost unique to every different input. Cryptographic hash functions like MD5, SHA-1, SHA-256 are widely used in several types of security applications.

3. Caching: Many caching strategies use hashing to quickly store and retrieve data. The distribution of keys into a cache can be based on a hash, so it's quick and easy to check if a key is (probably) in the cache or not.

4. Associative Arrays: Hashing is used to implement structures like dictionaries and Java's HashMap and HashSet, which allow fast lookup, insert and delete operations.

5. Load Balancing: Consistent hashing algorithms are used extensively in load balancing among distributed systems. A server or resource's identifier is hashed, and the resource is allocated based on that hash value.

6. Memoization: When a function result is expensive to compute and will be needed again, it can be useful to cache the result using a hash. Subsequent calls to the function with the same input can then simply look up the result in the cache.

7. Rabin-Karp algorithm: Rabin-Karp is a kind of string-searching algorithm that uses hashing to find patterns in strings.

In summary, hashing provides a way to uniquely identify and quickly access data. It's a cornerstone of many computer science fields like databases, computer networking, caching, cryptography, and more.

Heaps

Heaps are a type of tree-based data structure which follow a specific set of rules. In a max heap, each node's key is greater than or equal to the keys of its children. In a min heap, each node's key is less than or equal to the keys of its children.

Here are some practical uses of heap data structure:

1. Heap Sort: Heap sort algorithm uses the heap data structure to sort an array or list of elements. It first builds a max heap and then swaps the root node with end node (size of heap) and reduces the size of heap by one.

2. Priority Queue: Priority queues can be efficiently implemented using a binary heap because it supports insert, delete and extract highest operations efficiently. They are used in real time systems for scheduling jobs according to their priorities. An example of priority queue usage can be seen in emergency services, such as hospital emergency rooms where the patient with the most critical situation is served first, while the patient who doesn't need immediate medical attention waits. Here, the priority is determined by the severity of patients' medical conditions.

3. Graph Algorithms: Heaps are used in many famous graph algorithms such as Dijkstra's algorithm for finding the shortest path in a graph and Prim's algorithm to find the minimum spanning tree of a graph.

4. Order statistics: The heap data structure can be used to efficiently find the kth smallest (or largest) element in an array.

5. System Schedulers: In some instances, operating systems use heap data structures for load balancing and interrupt handling.

6. Resource Allocation in Simulations: In simulations, job queues often take the form of priority queues, where tasks are prioritized based on their importance or on simulation time.

Heaps provide a way to efficiently access the min or max element and insert with logarithmic performance which makes Heaps especially useful in applications where these kinds of operations are frequent.

Tries

Tries, also known as prefix trees or digital trees, are a kind of search tree data structure used to store a dynamic set or associative array where the keys are usually strings. In a trie, each node in the tree corresponds to a letter or character, storing data associated with a prefix of keys.

Here are some use cases for tries:

1. Autocomplete: Tries are well suited for building autocomplete features. They can efficiently provide all keys with a given prefix, making them ideal for implementing this feature in search engines or text editors.

2. Spell Check and Word Games: Tries can be used to validate the existence of a word in a dictionary. They can be used in word games like Scrabble and Boggle, or in writing software to provide spell checks.

3. IP Routing: Longest prefix matching, which is used to select an entry in a forwarding table, can be implemented using ternary search tries.

4. Text Mining: Tries can be used for tokenization of text in natural language processing and text analytics applications.

5. Efficient Search: If we want to search for all words from a dictionary that have a common prefix, we can do this very efficiently with the help of trie.

The trie data structure leverages the characteristics of the data set into its own structure. This makes it efficient to find whether a particular string or prefix exists in the data set by just traversing the trie.

Matrices

Matrices are a unique and valuable data structure, often used with arrays. A matrix is a grid of elements represented as rows and columns. It's technically a two-dimensional array, where each element is identified by two indices instead of just one. The practical applications of matrices are vast and significant, especially in the fields of computer graphics, physics, cryptography, and more:

1. Computer Graphics: Matrices are heavily utilized in computer graphics to transform geometric models into different coordinate systems. For instance, when rotating, translating, or scaling a 3D model, matrices are used to perform these operations smoothly.

2. Physics Simulations: Matrices are used in physics to represent states of physical systems, carry out transformations, and more. For example, in physics-related game development, matrices would have a substantial role in processing the game physics.

3. Cryptography: In cryptography, matrices can be used for encoding and decoding purposes. One of the well-known cryptographic methods using matrices is the Hill Cipher.

4. Machine Learning and Data Science: Matrices can represent datasets with multiple dimensions. They are instrumental in machine learning and statistical methods, where handling high-dimensional data is common. Matrices are extensively used in different stages of machine learning, including model training, representation of datasets, feature extraction, and more.

5. Mathematical Computations: Matrices are used in a variety of mathematical computations like solving systems of linear equations, finding determinants, eigenvalues, and eigenvectors of a system and so on.