Implementing a Binary Search Tree in Go

💡 Tree

• A tree is a non-linear data structure that simulates a hierarchical tree structure with a set of linked nodes. It has one root node and zero or more subtrees.

• A binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. Binary Search Tree (BST), also known as ordered or sorted binary tree, is a type of binary tree where the nodes are arranged in order: for each node, all elements in the left subtree are less than the node, and all elements in the right subtree are greater than the node.

👨‍🏫 Refer to my previous post about data structures if you are new to them, or check it out to learn about different types of tree structures.

---

Overview

BINARY SEARCH TREE

- 💡 contains: NODE (value, left, right)
- 📦 items: TREE (root)
- 🚦 methods: ADD (T), SEARCH (T), LENGTH, DEPTH, TRAVERSE, REMOVE (T)
TRAVERSE TYPES: IN-ORDER, PRE-ORDER, POST-ORDER, LEVEL-ORDER
IN-ORDER==DFS, LEVEL-ORDER==BFS
- ⚡️ extra: FLATTEN, TO-ARRAY, NEW-FROM-ARRAY

---

⭐️ In here, we use Go Generics and cmp.Ordered data type. You don’t need to have a prior knowledge of Go Generics syntaxes as this is a good example of usage of Generics and a good opportunity to get familiarize with Go Generics syntaxes.

Let’s get started.

Implementation

Binary Search Tree

type Node[T cmp.Ordered] struct {
	value T
	left  *Node[T]
	right *Node[T]
}

type BinarySearchTree[T cmp.Ordered] struct {
	root *Node[T]
}

Factory

func New[T cmp.Ordered]() *BinarySearchTree[T] {
	return &BinarySearchTree[T]{}
}

Add

func (t *BinarySearchTree[T]) Add(v T) {
	t.root = add(t.root, v)
}

func add[T cmp.Ordered](node *Node[T], v T) *Node[T] {
	if node == nil {
		return &Node[T]{value: v}
	}

	if v < node.value {
		node.left = add(node.left, v)
	} else if v > node.value {
		node.right = add(node.right, v)
	}

	return node
}

Search

func (t *BinarySearchTree[T]) Search(v T) (*Node[T], error) {
	return search(t.root, v)
}

func search[T cmp.Ordered](node *Node[T], v T) (*Node[T], error) {
	if node == nil {
		return nil, ErrNotFound
	}

	if v < node.value {
		return search(node.left, v)
	} else if v > node.value {
		return search(node.right, v)
	}

	return node, nil
}

var ErrNotFound = errors.New("not found")

Length

func (t *BinarySearchTree[T]) Length() int {
	count := 0

	var countNodes func(*Node[T])
	countNodes = func(node *Node[T]) {
		if node != nil {
			count++
			countNodes(node.left)
			countNodes(node.right)
		}
	}

	countNodes(t.root)

	return count
}

Depth

func (t *BinarySearchTree[T]) Depth() int {
	var maxDepth func(node *Node[T]) int
	maxDepth = func(node *Node[T]) int {
		if node == nil {
			return 0
		}

		leftDepth := maxDepth(node.left)
		rightDepth := maxDepth(node.right)

		if leftDepth > rightDepth {
			return leftDepth + 1
		}
		return rightDepth + 1
	}

	return maxDepth(t.root)
}

---

Traversal methods

Traversals are the process/order of visiting each node of a tree or graph. There are mainly 4 ways of traversing items of the tree. Let’s consider the following tree.

1. In-order (Depth-First Search/ DFS)
   traversal: left-node-right
   result: 1 -> 2 -> 3 -> 5 -> 6

2. Pre-order
   traversal: node-left-right
   result: 5 -> 2 -> 1 -> 3 -> 6

3. Post-order
   traversal: left-right-node
   result: 1 -> 3 -> 2 -> 6 -> 5

4. Level-order (Breadth-First Search/ BFS)
   traversal: level by level(node-left-right)
   result: 5 -> 2 -> 6 -> 1 -> 3

Traverse in-order

func (t *BinarySearchTree[T]) TraverseInOrder() string {
	return inOrder(t.root, "")
}

func inOrder[T cmp.Ordered](node *Node[T], str string) string {
	if node == nil {
		return str
	}

	str = inOrder(node.left, str)
	str = fmt.Sprintf("%s%v ", str, node.value)
	str = inOrder(node.right, str)

	return str
}

Traverse pre-order

func (t *BinarySearchTree[T]) TraversePreOrder() string {
	return preOrder(t.root, "")
}

func preOrder[T cmp.Ordered](node *Node[T], str string) string {
	if node == nil {
		return str
	}

	str = fmt.Sprintf("%s%v ", str, node.value)
	str = preOrder(node.left, str)
	str = preOrder(node.right, str)

	return str
}

Traverse post-order

func (t *BinarySearchTree[T]) TraversePostOrder() string {
	return postOrder(t.root, "")
}

func postOrder[T cmp.Ordered](node *Node[T], str string) string {
	if node == nil {
		return str
	}

	str = postOrder(node.left, str)
	str = postOrder(node.right, str)
	str = fmt.Sprintf("%s%v ", str, node.value)

	return str
}

Traverse level-order

func (t *BinarySearchTree[T]) TraverseLevelOrder() (str string) {
	if t.root == nil {
		return
	}

	queue := []*Node[T]{t.root}
	for len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]
		str = fmt.Sprintf("%s%v ", str, node.value)

		if node.left != nil {
			queue = append(queue, node.left)
		}

		if node.right != nil {
			queue = append(queue, node.right)
		}
	}

	return
}

---

Remove

func (t *BinarySearchTree[T]) Remove(v T) error {
	var found bool

	if t.root, found = remove(t.root, v); !found {
		return ErrNotFound
	}
	return nil
}

func remove[T cmp.Ordered](node *Node[T], v T) (*Node[T], bool) {
	if node == nil {
		return nil, false
	}

	var found bool
	if v < node.value {
		node.left, found = remove(node.left, v)
	} else if v > node.value {
		node.right, found = remove(node.right, v)
	} else {
		if node.left == nil && node.right == nil {
			return nil, true
		}

		if node.left == nil {
			return node.right, true
		}

		if node.right == nil {
			return node.left, true
		}

		minValueNode := findMinNode(node.right)

		node.value = minValueNode.value
		if node.right == minValueNode {
			node.right = minValueNode.right
		} else {
			node.right, _ = remove(node.right, node.value)
		}

		found = true
	}

	return node, found
}

func findMinNode[T cmp.Ordered](node *Node[T]) *Node[T] {
	current := node

	for current != nil && current.left != nil {
		current = current.left
	}

	return current
}

---

⚡️ Let’s see how to implement extra functionalities which are not directly related to this data structure.

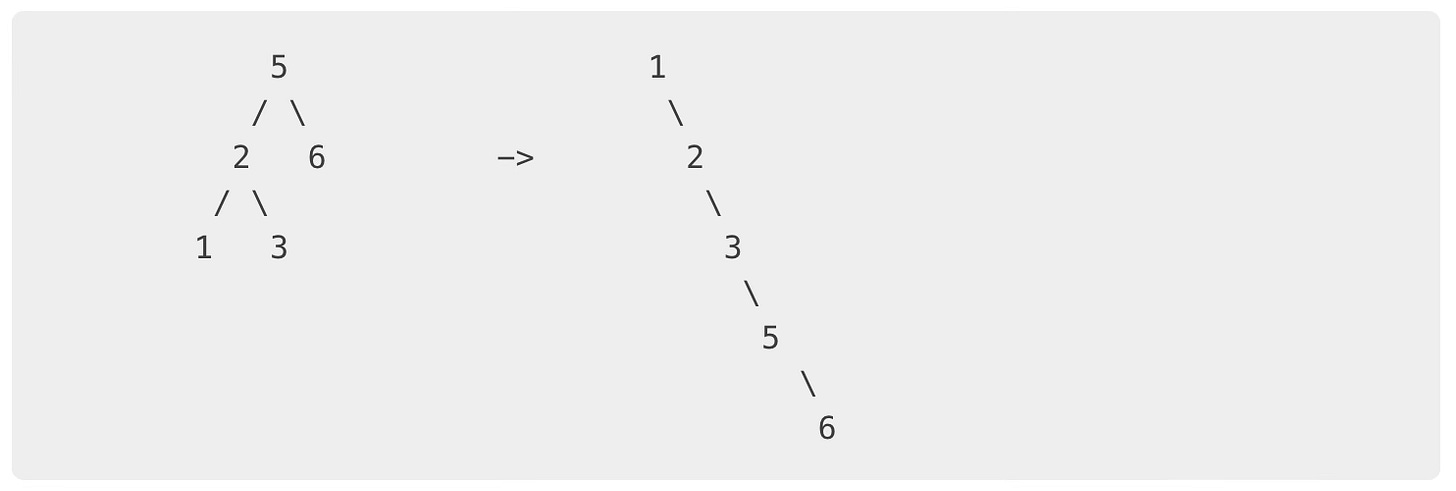
Flatten

Flatten in-order

func (t *BinarySearchTree[T]) FlattenInOrder() {
	head := &Node[T]{}
	current := head

	var flatten func(*Node[T])
	flatten = func(node *Node[T]) {
		if node != nil {
			flatten(node.left)
			node.left = nil
			current.right = node
			current = node
			right := node.right
			flatten(right)
		}
	}

	flatten(t.root)
	t.root = head.right
}

Flatten level-order

func (t *BinarySearchTree[T]) FlattenLevelOrder() {
	if t.root == nil {
		return
	}

	queue := []*Node[T]{t.root}
	head := &Node[T]{}
	current := head

	for len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]

		current.right = node
		current.left = nil
		current = current.right

		if node.left != nil {
			queue = append(queue, node.left)
		}
		if node.right != nil {
			queue = append(queue, node.right)
		}
	}

	current.right = nil
	t.root = head.right
}

To Array

func (t *BinarySearchTree[T]) ToArray() []T {
	result := make([]T, 0, t.Length())

	var traverse func(*Node[T])
	traverse = func(node *Node[T]) {
		if node != nil {
			traverse(node.left)
			result = append(result, node.value)
			traverse(node.right)
		}
	}

	traverse(t.root)

	return result
}

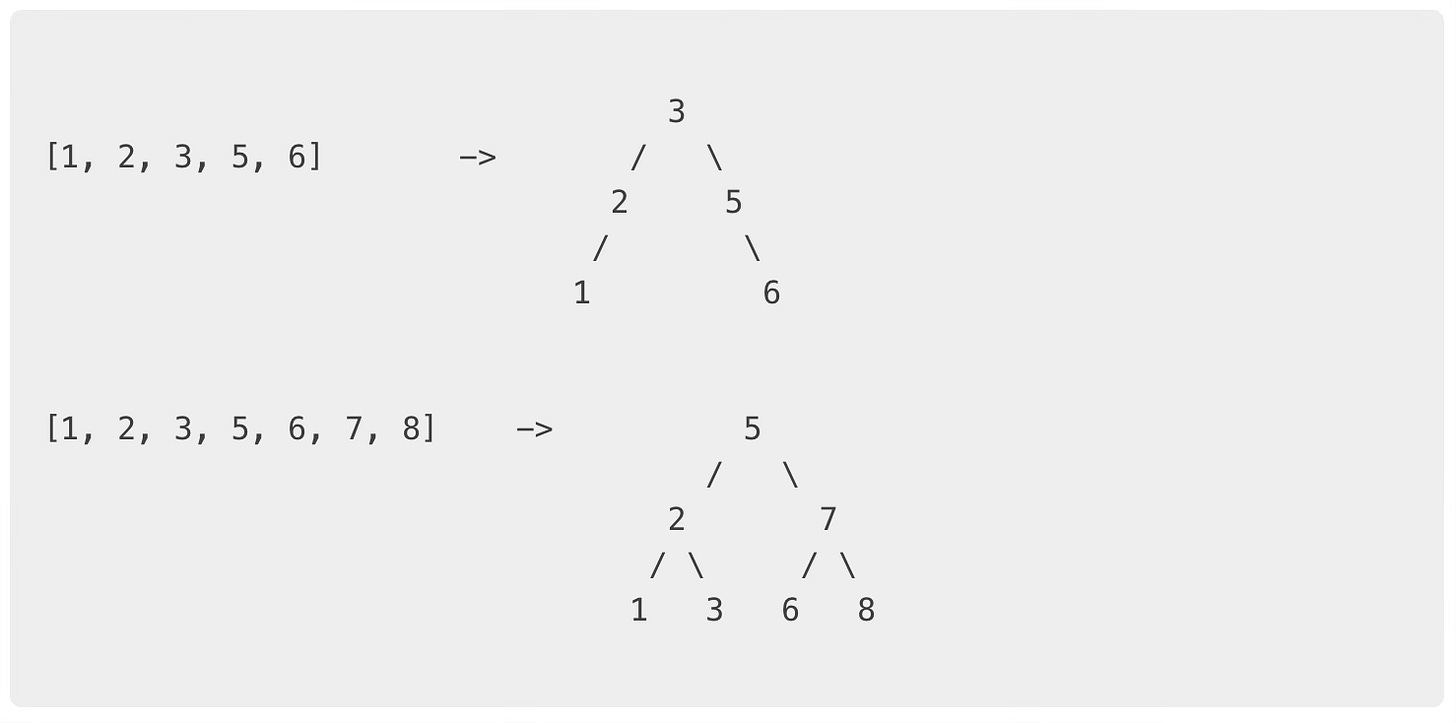
Factory From Array

func NewFromArray[T cmp.Ordered](elements []T) *BinarySearchTree[T] {
    tree := &BinarySearchTree[T]{}
    tree.root = addFromSortedArray(elements, 0, len(elements)-1)
    return tree
}

func addFromSortedArray[T cmp.Ordered](elements []T, start int, end int) *Node[T] {
    if start > end {
       return nil
    }

    mid := (start + end) / 2
    node := &Node[T]{value: elements[mid]}

    node.left = addFromSortedArray(elements, start, mid-1)
    node.right = addFromSortedArray(elements, mid+1, end)

    return node
}

---

⭐️ To practice further, add following new methods to the binary search tree

• IS-BALANCED : to verify the tree is balanced